第738节(2/3)

到底要告诉我们什么？”

因为轰击的电会传递一分能量给另一个电，从而导致其能量提，粒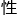变得更明显，半径就会更小。

“模糊的能量场。”李谕说。

李谕耸耸肩：“已经没有其他办法了。只能假设电只有半径，但没有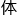积，甚至没有边界，更不会有结构。”

后来理学家就是用的这个办法去测量电半径。但实验结果却让人瞠目结，异常诡异：

李谕说：“说不定就是这样，至少数学上可以这么理。用不了多久，英国的狄拉克先生估计就会写他的新论文———他在布鲁尔时是这么说的。”

据此推测，电或许就是个模糊不清的能量场。因此你要是说它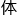积无限大，貌似也不完全错。

李谕摊手：“目前的条件肯定不了这么准的实验。”

直到波近康普顿波这个限。

本章尚未读完,请击一页继续阅读---->>>

李谕说：“依我看，概率是个好东西。概率是什么？是不确定，是模糊不清。所以，我认为电说不定不是一个常规认为的实心小球。”

冯·诺依曼此时反而没有那么惊讶：“院士先生也想用数学来理理学？”

“既然可以是波，那么电就有可能双实验，甚至单电的双实验，想想就不寒而栗！”

李谕说：“只有这样假设，很多事才能说得清。你还记得因斯坦教授关于宇宙有限无界的说法吗？”

冯·诺依曼：“当然知。”

如果要测量更确的半径，就要用更能量的电轰击，半径就会更小，陷死循环。

这个理论可以用于解释量纠缠：因为这两个分裂的粒，用的本来就是一个能量场，你对其中一个

从实验的角度，用电轰击电，再通过散角度确实可以推测电的半径。

冯·诺依曼赞同说：“微观领域太神奇了，比任何冒险都有趣得多，因为那里满满都是未知。我看到已经有人成功电散实验，证明了电有波的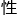质，这简直太恐怖了！”

李谕笑：“面肯定暗涌动。”

冯·诺依曼大惊：“怎么可能！”

被测量的电的半径，会随着轰击电的能量大小而变化！

“要是现在什么都知，就没意思了。”李谕轻松。

“单电！它要自己同自己涉？”

“有意思！”冯·诺依曼说，“不过我暂时还无法接受电没有结构的说法。”

冯·诺依曼说：“可惜我不懂实验，不然真想利用电的衍来测量一电半径，看看是不是如先生的理论推导那样。”

“院士先生的察力世所罕见，竟然在这么短的一堂普通数学研讨会上就看了我的方向，”冯·诺依曼很惊讶，然后承认，“没错，我想知在这些优雅的数学之究竟发生了什么。”

冯·诺依曼说：“那不就成了零维度的粒，本不占据空间，只是一个？”

所以理学家才猜测，电很可能作为基本粒，并没有结构，或者换个更严谨的说法，电的结构对于我们来说是未知的。

也就是说，电的半径无法测量得很确。嗯，又是波粒二象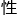和不确定原理在作祟。

“微观粒也可以借用类似的假想，”李谕说，“电可能就是一有半径无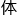积的模糊的……”

“模糊的什么？”冯·诺依曼问。

这个问题困扰了理学家很多年，但不包括李谕在……