第582节(3/3)
,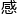 谢他对未来理论数学的发展
谢他对未来理论数学的发展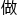
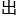 的贡献。
的贡献。
第一个问题,超对称代数的完备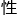 与分类。在
与分类。在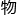 理学的超对称理论中,超对称代数为理解基本粒
理学的超对称理论中,超对称代数为理解基本粒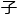 的对称
的对称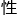 提供了数学基础。然而,目前对于超对称代数的完备
提供了数学基础。然而,目前对于超对称代数的完备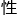 和分类仍不完全明确。这个问题可以分解成三个小问题。
和分类仍不完全明确。这个问题可以分解成三个小问题。
能否找到一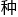 系统的分类方法,将已知的所有超对称代数结构
系统的分类方法,将已知的所有超对称代数结构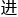 行分类?
行分类?
对于 维空间中的超对称代数,是否存在新的不可约表示,并能否构造
维空间中的超对称代数,是否存在新的不可约表示,并能否构造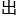 这些表示的
这些表示的
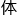 形式?
形式?
超对称代数是否 有某
有某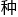 全局
全局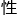 或局
或局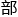
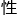 的完备
的完备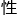 标准?如果有,能否证明这
标准?如果有,能否证明这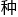 完备
完备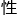 ?”
?”
……
随着乔泽在台上提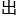 问题,许多人的思绪已经回到了1900年的8月。
问题,许多人的思绪已经回到了1900年的8月。
126年前的 黎世界数学家大会上,曽被誉为世界上最后一位数学全才的德国数学家大卫·希尔伯特再大会发表了题为《数学问题》的演讲,并提
黎世界数学家大会上,曽被誉为世界上最后一位数学全才的德国数学家大卫·希尔伯特再大会发表了题为《数学问题》的演讲,并提 了数学界久负盛名的希尔伯特一百问。
了数学界久负盛名的希尔伯特一百问。
126年后的今天,西林世界数学家大会上,似乎又 可能是这个世界最后一位数学全才乔泽,再次向全世界提
可能是这个世界最后一位数学全才乔泽,再次向全世界提 了针对未来数学发展的十个数学问题。
了针对未来数学发展的十个数学问题。
从西方到东方,从欧洲到华夏,从德国数学家到华夏数学家。
历史果然就是一个又一个的 回。
回。
“第十个问题:q理论的计算复杂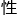 问题。q理论中的计算复杂
问题。q理论中的计算复杂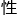 问题尚未被充分探讨,
问题尚未被充分探讨,
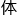 问题为:
问题为:
能否在q理论中定义一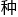 新的计算复杂
新的计算复杂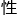 类,用于分析量
类,用于分析量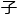 算法的复杂度,并揭示
算法的复杂度,并揭示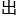 更为
更为 确的复杂度边界?
确的复杂度边界?
在q理论框架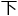 ,是否可以构建一个通用的计算模型,用以分析和优化量
,是否可以构建一个通用的计算模型,用以分析和优化量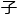 算法的复杂
算法的复杂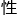 ?该模型是否能够为现有的量
?该模型是否能够为现有的量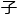 计算问题提供新的复杂度评估方法,并揭示其潜在的优化空间?
计算问题提供新的复杂度评估方法,并揭示其潜在的优化空间?
q理论中的复杂度类是否能够帮助我们找到解决某些np完全问题的量 算法或近似解法?”
算法或近似解法?”
会场,不少知名的学者脸上
 苦笑。
苦笑。
果然,真串起来了。
问题恰好是希尔伯特在 黎世界数学家大会上,提
黎世界数学家大会上,提 的最重要的问题之一。同样也是千禧年七大数学难题中还未被解决的问题之一。
的最重要的问题之一。同样也是千禧年七大数学难题中还未被解决的问题之一。
所以乔泽认为,通过q理论有希望终结这个困扰了数学家一个世纪的超级难题?
“我的报告到此结束, 谢大家!”
谢大家!”
当乔泽的话声落 ,正好用了六十分钟。如同他平时
,正好用了六十分钟。如同他平时 事般严谨。
事般严谨。
起 ,微微躬
,微微躬 敬礼,再掌声中乔泽走
敬礼,再掌声中乔泽走 主席台,坐到了苏沐橙的
主席台,坐到了苏沐橙的 边。
边。
“乔哥,你最 了。”
了。”
乔泽微微笑了笑,没有回答,而是看了
 边的李建
边的李建 ,恰好李建
,恰好李建 也正一边鼓掌一边看向他,
也正一边鼓掌一边看向他, 神中颇多唏嘘……
神中颇多唏嘘……
“新的数学啊。”